Engineering Math Test
For jobseekers
Practice your skills and earn a certificate of achievement when you score in the top 25%.
Take a Practice TestFor companies
Test candidates with real-world problems and interview the best ones.
Sign Up to Offer this TestAbout the test
The Engineering Math test assesses the ability to solve engineering mathematics problems.
The assessment includes solving work-sample tasks, such as:
- Calculating probability and number of combinations for different scenarios.
- Summarizing data from charts by calculating the mean, median, and standard deviation.
- Turning complex problems into a set of linear equations and solving them.
Good data analysts, mechanical engineers, and software developers all need a solid understanding of engineering mathematics to effectively analyze data, design mechanical systems, and develop software that solves complex problems and enhances operational efficiency.
Sample public questions
Before purchasing seeds, a farmer needs to know the area of his land. Since one end of his property is currently unapproachable, he measured only three sides. This is his sketch with measurements:
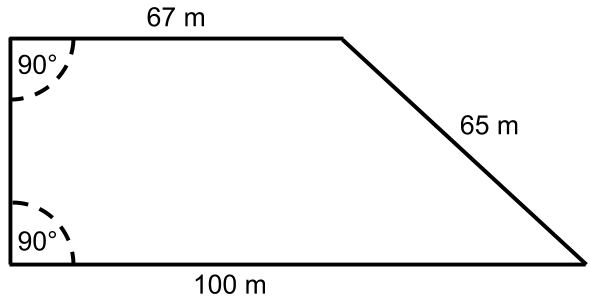
What is the area of the land?
An HR department analyzed the years of work experience of the company's two largest departments: Production and R&D. Based on the analysis the following report was produced:
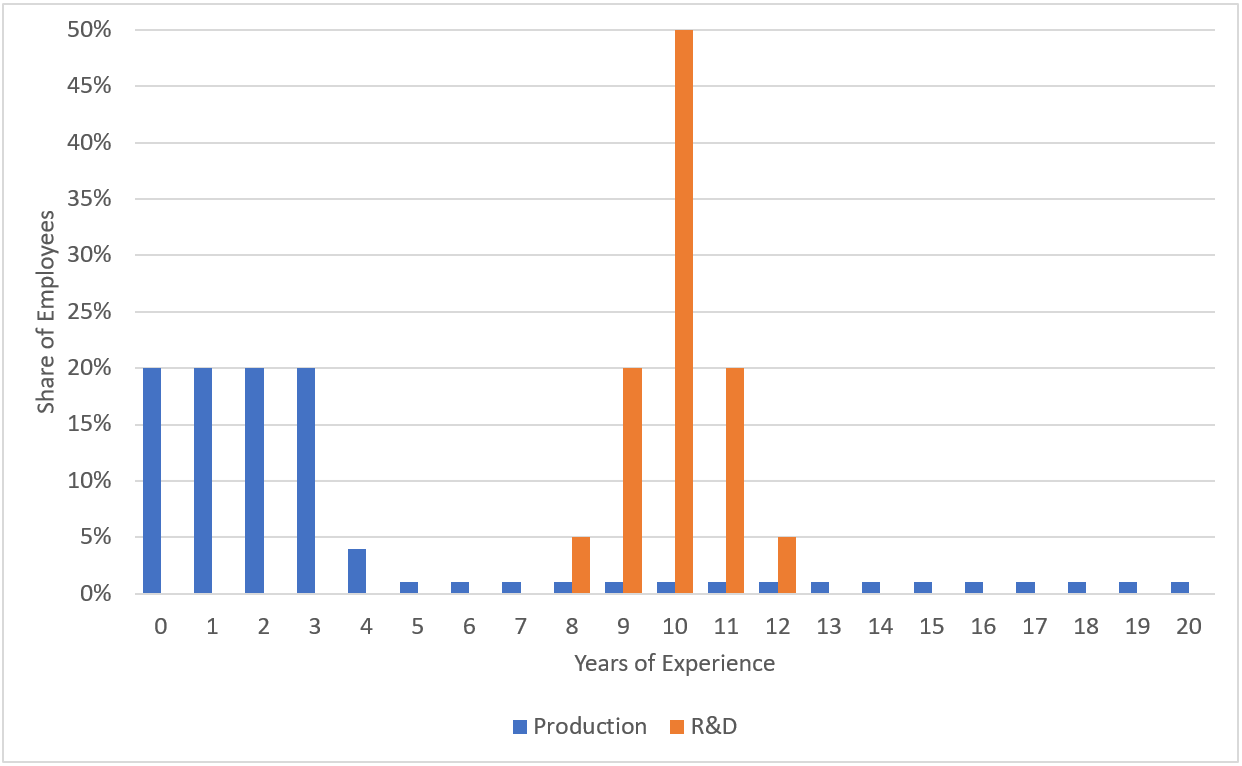
What can be concluded about the years of experience for each department?
For jobseekers: get certified
Earn a free certificate by achieving top 25% on the Engineering Math test with public questions.
Take a Certification TestSample silver certificate
Sunshine Caprio
Java and SQL TestDomeCertificate
For companies: premium questions
Buy TestDome to access premium questions that can't be practiced.
Get money back if you find any premium question answered online.
13 more premium Engineering Math questions
Classification Yard, Attic, Handbarrow, Sensor Set, Chocolate Box, Bouquet of Roses, Overtime, Roulette, Car Velocity, Contest Idea, Fraction Equation, Car Acceleration, Accelerometer.
Skills and topics tested
- Engineering Math
- Combinatorics
- Permutation
- Geometry
- Trigonometry
- Volume
- Linear Algebra
- Linear Equations
- Vectors
- Probability
- Without Replacement
- Combination
- Median
- Mode
- Quartile
- Statistics
- Independent Events
- Calculus
- Integration
- Nonlinear System
- Polynomial Function
- Arithmetic
- Fractions
- Derivation
- Function Extrema
- Matrix
- Matrix Addition
- Scalar Multiplication
For job roles
- Data Analyst
- Mechanical Engineer
- Software Developer
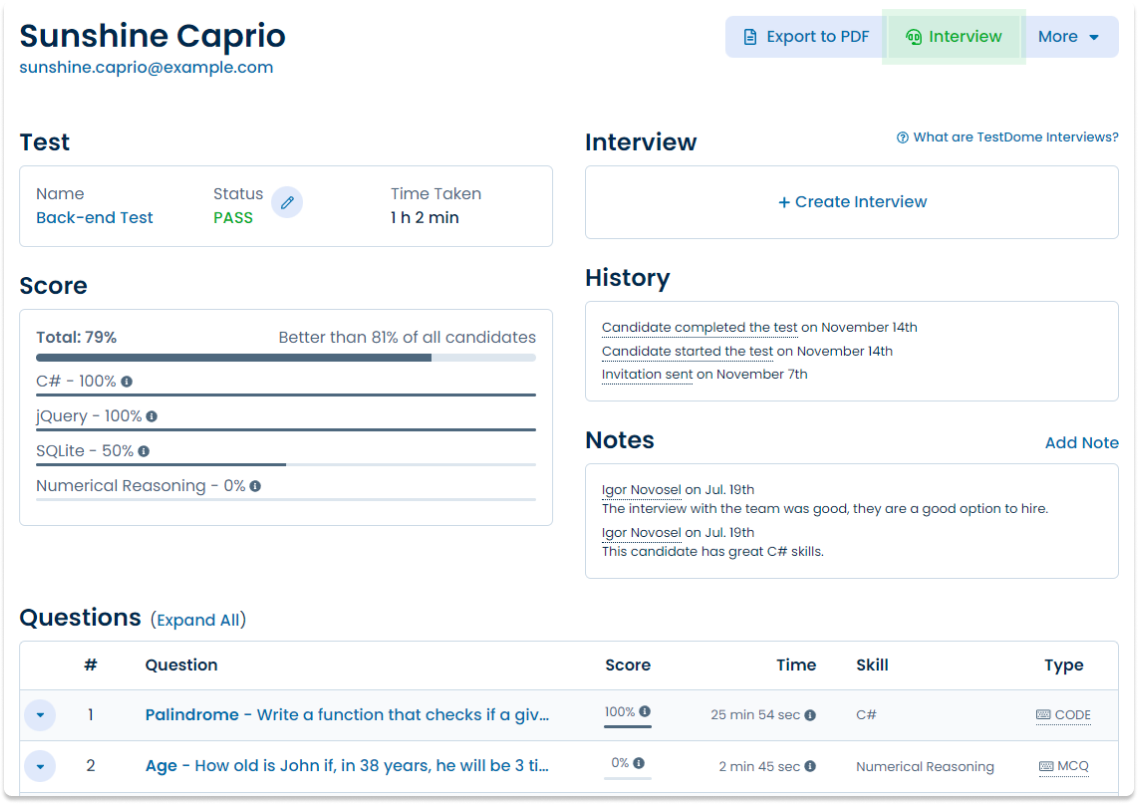
Sample candidate report
Need it fast? AI-crafted tests for your job role
TestDome generates custom tests tailored to the specific skills you need for your job role.
Sign up now to try it out and see how AI can streamline your hiring process!
What others say
Simple, straight-forward technical testing
TestDome is simple, provides a reasonable (though not extensive) battery of tests to choose from, and doesn't take the candidate an inordinate amount of time. It also simulates working pressure with the time limits.
Jan Opperman, Grindrod Bank
Product reviews
Used by
Solve all your skill testing needs
150+ Pre-made tests
130+ skills
Multi-skills Test
How TestDome works
Choose a pre-made test
or create a custom test
Invite candidates via
email, URL, or your ATS
Candidates take
a test remotely
Sort candidates and
get individual reports
