Python Online Test
For jobseekers
Practice your skills and earn a certificate of achievement when you score in the top 25%.
Take a Practice TestFor companies
Screen real Python skills, flag human or AI assistance, and interview the right people.
About the test
The Python online test assesses knowledge of programming in the Python language and commonly used parts of the Python Standard Library. This test requires solving live coding problems in Python.
The assessment includes work-sample tasks such as:
- Working with Python collections and language constructs.
- Using proper algorithms and data structures to optimize application performance.
- Serializing to/from JSON to handle web requests.
A good Python developer needs a solid understanding of the Python programming language and knowledge of its data structures and language constructs to write robust and maintainable code.
Sample public questions
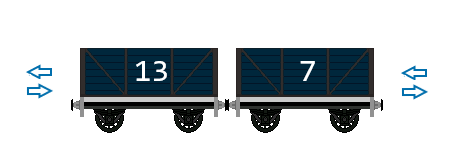
Your company is analyzing malware that targets numerical record files stored in an array.
The malware adjusts values at both the edges of the array using a window of size 's' as shown in the video below:
Implement the simulate method so that the malware behavior is replicated for further study.
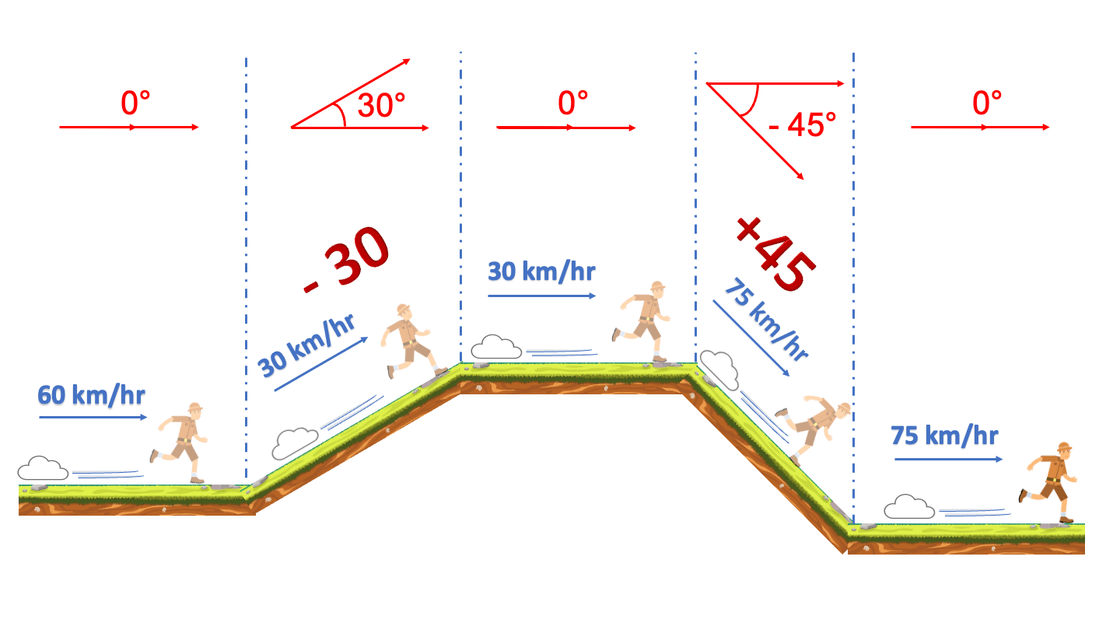
A megastore offers three types of discounts, which are represented as DiscountType enum.
Implement the get_discounted_price function which should take the total weight of the shopping cart, the total price, and the discount type. It should return the final discounted price based on the discount schemes as shown in the promotional video below:
(Open full-size video in a new tab)
For example, the following code:
print(get_discounted_price(12, 100, DiscountType.WEIGHT))should print:
82.0For jobseekers: get certified
Earn a free certificate by achieving top 25% on the Python test with public questions.
Take a Certification TestSample silver certificate
Sunshine Caprio
Java and SQL TestDomeCertificate
For companies: premium questions
Buy TestDome to access premium questions that can't be practiced.
Ready to interview?
Use these and other questions from our library with our
Code Interview Platform.
75 more premium Python questions
Category Tree, Kilometer Converter, Chain Link, Unique Numbers, Moving Total, Max Sum, Reward Points, Flight Connections, Internal Nodes, Is Alpha, Hobbies, Medical Record, Read First Line, Crop Ratio, Username, Log Parser, Veterinarian, Segment, Language Teacher, Read Write Execute, Ceramic Store, String Occurrence, Book Sale, Numbers To Text, Log Patch, Count Hobbies, Book Authors, Friend, Car Rental, Chinese Box, Stories, Driver Exam, Worker, Vectors, Random Playlist, File Format, Action Stack, Paragraph, Cargo Ship, Tuple Slice, Greeter, Node, Students, Calories Burned, Paper Strip, Construction Game, Date Transform, Special Actions, Chemical Machine, Adventure Game, Seasonal Tourism, Candies, Digital Flasks, Shipping, Procedural Generator, Flimsy Bridge, Parking Allocation, Planet Search, Ecological Experiment, Company Stock, Automated Forklift, Popular Book, Circuit Simulator, Airport Networks, Document Store, Jobs Time, Christmas Lights, Movie Night, Automated Warehouse, Fraud Detection, Pet Names, Mail Room, Weather Station, Newest User, Price Trends.
Skills and topics tested
- Python
- Dictionary
- Exceptions
- Inheritance
- Method Overriding
- OOP
- Linked List
- Algorithmic Thinking
- Set
- Graphs
- Lists
- Tree
- List Comprehension
- Strings
- Iteration
- Named Tuple
- Bug Fixing
- Integer Division
- Language
- Regex
- Serialization
- XML
- Queue
- Arithmetic
- Multithreading
- Stream
- Sorting
- Monkey Patching
- Conditions
- Performance Tuning
- Data Structures
- Dynamic Programming
- Memory Management
- Closures
- Stack
- Tuples
- Recursion
- JSON
- Video
- Random
- AI Code Review
- Conditional Statements
- Loops
- 2D Array
- Classes
For job roles
- Back-End Developer
- Python Developer
- Web Developer
Sample candidate report
Need it fast? AI-crafted tests for your job role
TestDome generates custom tests tailored to the specific skills you need for your job role.
Sign up now to try it out and see how AI can streamline your hiring process!
What others say
Simple, straight-forward technical testing
TestDome is simple, provides a reasonable (though not extensive) battery of tests to choose from, and doesn't take the candidate an inordinate amount of time. It also simulates working pressure with the time limits.
Jan Opperman, Grindrod Bank
Product reviews
Used by
Solve all your skill testing needs
150+ Pre-made tests
130+ skills
AI-ready assessments
How TestDome works
Choose a pre-made test
or create a custom test
Invite candidates via
email, URL, or your ATS
Candidates take
a test remotely
Sort candidates and
get individual reports

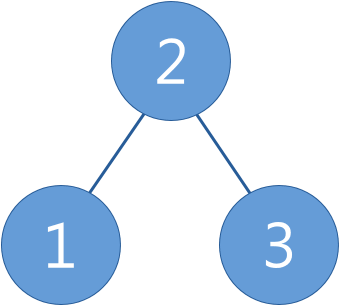 Binary search tree (BST) is a binary tree where the value of each node is larger or equal to the values in all the nodes in that node's left subtree and is smaller than the values in all the nodes in that node's right subtree.
Binary search tree (BST) is a binary tree where the value of each node is larger or equal to the values in all the nodes in that node's left subtree and is smaller than the values in all the nodes in that node's right subtree.